IPアドレスから地理的位置情報(GeoIPLocation)の検索機能を公開しました。
255までの数値を紙とペンでビットパターンに変換する方法
IPアドレスの計算やビットパターンの確認では、
Windows電卓やツールなどを利用すると簡単です。
しかし、そうしたツールがない状態でビットパターンを求めたい場合には、
紙とペンを使って計算で求めることもできます。
ここでは２５５までの数値を単純作業でビット化する手順をご紹介します。
この方法はあくまでも自己流です。
もっと簡単な方法があったらTwitterなどで教えてください。
この方法は引き算しかしないので、ミスは少ないと思いますが。
目次
255までの数値を紙とペンでビットパターンに変換する方法
試験会場などで、問題用紙の空きスペースで、
ちょっとビットパターンを確認したい場合には、
以下のように紙に書きながら、単純作業でビットを求めます。
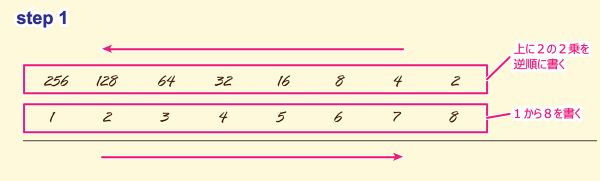
STEP1
まず、左から１～８の数字を書きます。
次にその上にでも、右から２の乗数を順に書きます。
この値を利用して計算していきます。
01_ベースの値を準備ステップ１
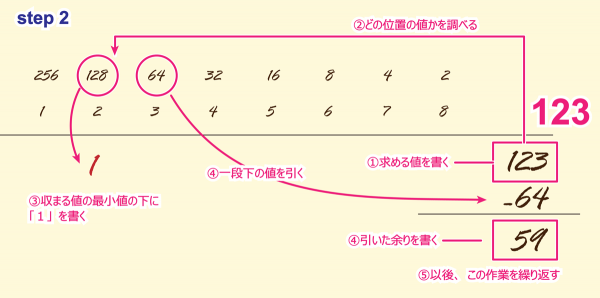
STEP2
①次に求めたい数値を右にでも書きます。
ここでは「１２３」のビットパターンを求めることとします。
②次に123が各２乗の値の中で納まる位置を探します。
比較は以下の式で行います。
2^n => NUM > 2^n-1
※下側の値に一致した場合は、上を採用します。
「１２８」が上の値です。
「６４」が下の値になります。
③対象の値が収まる範囲の上側の数値の下に「１」を書きます。
④対象の値が収まる範囲の下側の値「６４」を、求める値の下に書き、
マイナスを付けて引き算します。
⑤引いた余りを求めて書きます。「１２３－６４＝５９」
次は求める値を「５９」から再び開始します。
この作業の繰り返しを行います。
本当に単純作業です。
最後が１桁になるまで繰り返します。
02_求める値を記載計算ステップ２
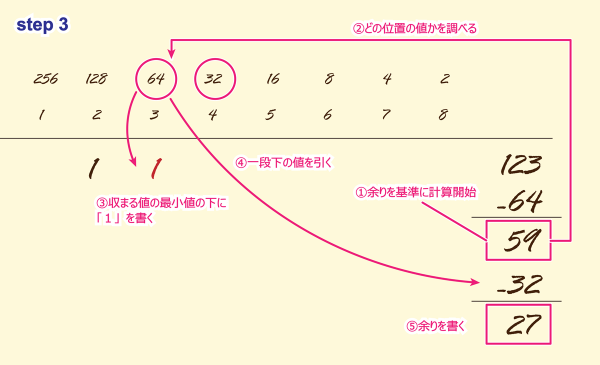
STEP3
①「５９」が収まる位置を求めます。
②上が「６４」下が「３２」です。
③上の値「６４」の下に「１」を書きます。
④下の値「３２」を求める値から引き算します。
⑤余りは「５９－３２＝２７」です。
03_求める値を減算で求め計算ステップ３
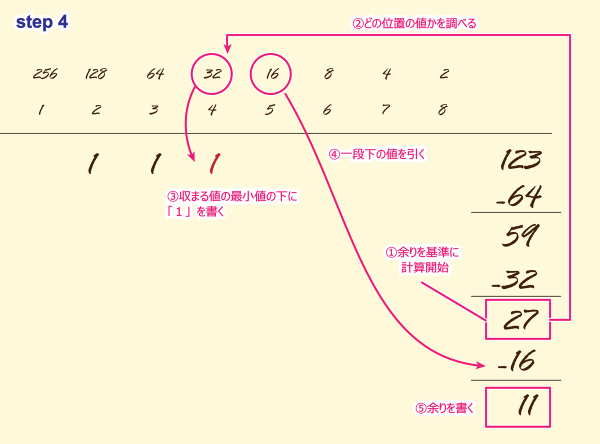
STEP4
①「２７」が収まる位置を求めます。
②上が「３２」下が「１６」です。
③上の値「３２」の下に「１」を書きます。
④下の値「１６」を求める値から引き算します。
⑤余りは「２７－１６＝１１」です。
04_求める値を減算で求め計算ステップ４
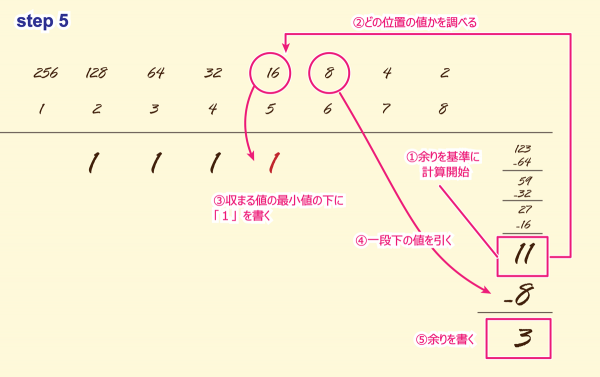
STEP5
①「１１」が収まる位置を求めます。
②上が「１６」下が「８」です。
③上の値「１６」の下に「１」を書きます。
④下の値「８」を求める値から引き算します。
⑤余りは「１１－８＝３」です。
05_求める値を減算で求め計算ステップ５
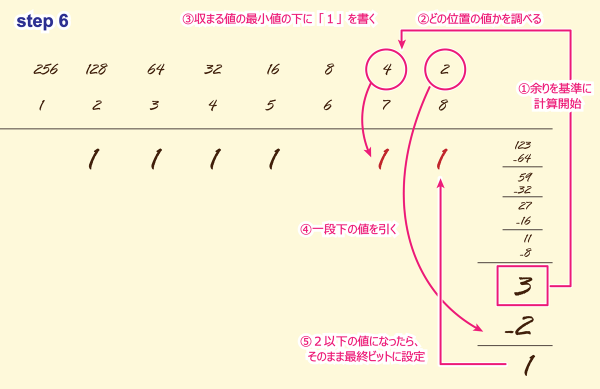
STEP6
①「３」が収まる位置を求めます。
②上が「４」下が「２」です。
③上の値「４」の下に「１」を書きます。
④下の値「２」を求める値から引き算します。
⑤余りは「３－２＝１」です。
ここで解が１桁になりました。
ここで求まった１桁は最終ビットになります。
一番右にそのまま書きます。
これでビットの１が立つ部分が求まりました。
06_求める値を減算で求め計算ステップ６
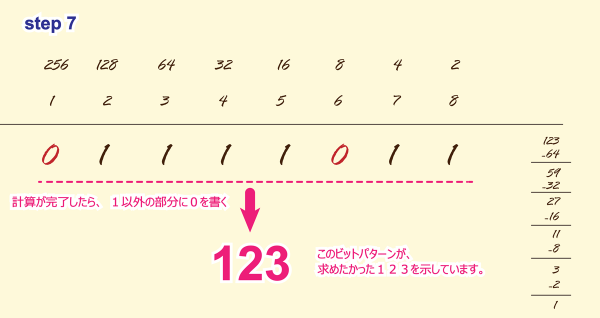
STEP7
「１」が立たなかった部分すべてに「０」を書きます。
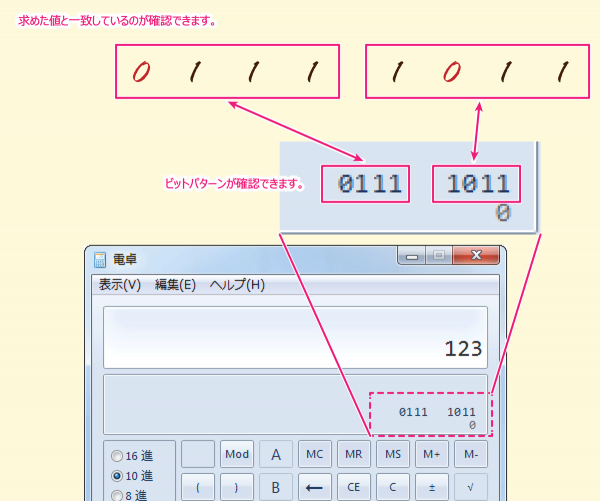
ズバリ、このビットパターンが、
求めたかった値の「１２３」を示しています。
「0111 1011」
07_空ビットに０を記入し完成
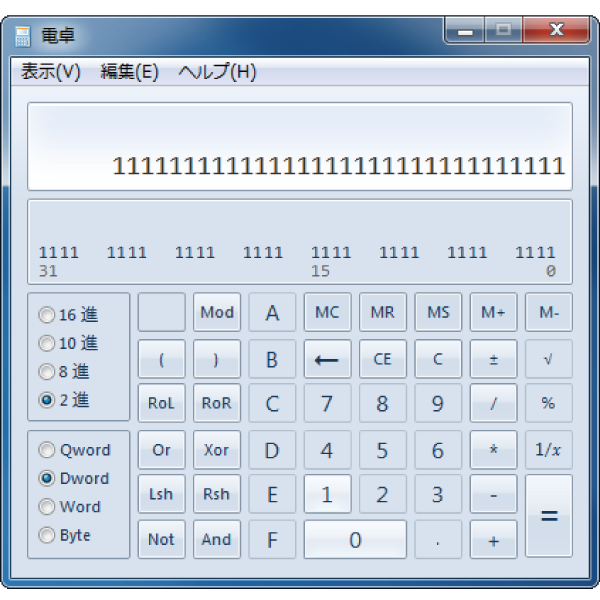
Windows電卓で確認します。
確認方法は以下でご紹介しています。
「１２３」と入力した、直下に表示されているビットパターンと、
求めたパターンは一致しています。
08_「１２３」の検算
正しく求められています。
最終チェックとして確認する点として以下を確認します。
奇数は最終ビットが「１」
偶数は最終ビットが「０」になります。
その為「１２３」の時点で最終ビットは「１」が分かっています。
先に「１」と立てておくことで、
最後に求めた値とビットが一致していれば、計算はほぼOKと言えます。
このことからもわかるように、
ネットワークIPアドレス(ホスト部の下位ビットがすべて０)は、
必ず偶数ということも言えます。
偶数の場合の例
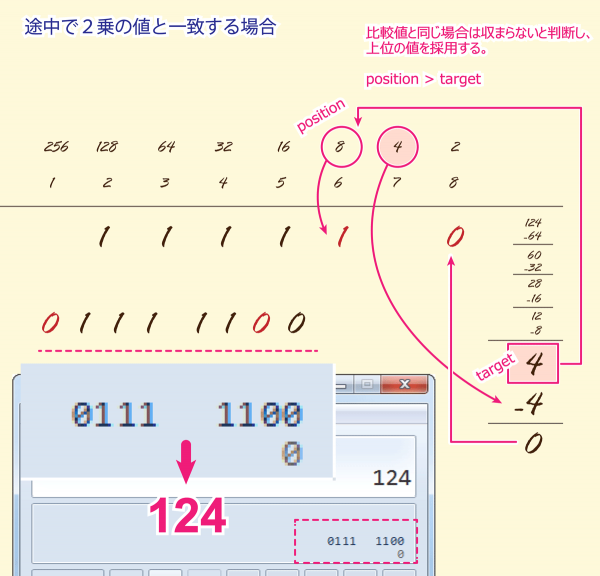
次に偶数の場合として１を加えた「１２４」を見てみます。
この場合も手順は同じですが、
「１２４」では４回目の時に「４」が求める値になります。
４は「２の２乗」に一致することになります。
しかし、求める式では「＞」です。
2^n => NUM > 2^n-1
よって、採用される位置は「８=> （位置） > 4」となり、
上が８、下が４になります。
「８」の下に「１」を書き、下の値「４」で引き算すると、
解が「０」となり、１桁になります。
１桁になったら、それは最終ビットにして計算終了です。
求めたビットパターンは「0111 1100」で「１２４」になっています。
「１２３」＝「0111 1011」でしたから、
１を加算すると繰り上がって「0111 1100」となりますので、
辻褄も合っています。
09_「１２４」の場合の偶数パターン
こうして偶数の場合には、スコーンと「０」のタイミングが現れて、
計算終了という形になるわけです。
本当かいな？という方へ
まぁ、私も何となくこの方法を見つけた時は、
本当かいなと思ったのですが、ちゃんと求められるんですね。
以下は疑い深い方向けに・・・
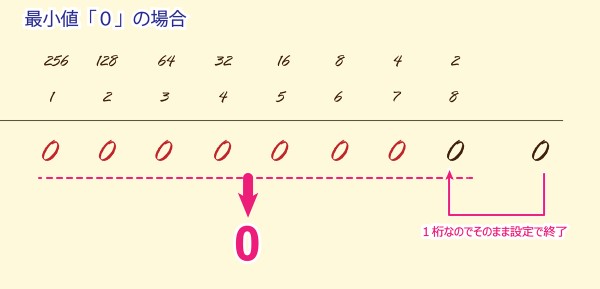
「０」の場合
当然、１桁なので最終ビットに「０」で終了
10_「０」の場合
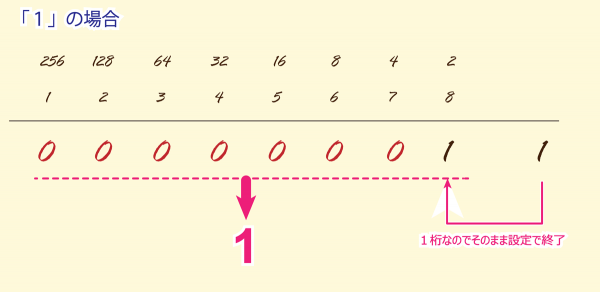
「１」の場合
同じく、１桁なので最終ビットに「１」で終了
11_「１」の場合
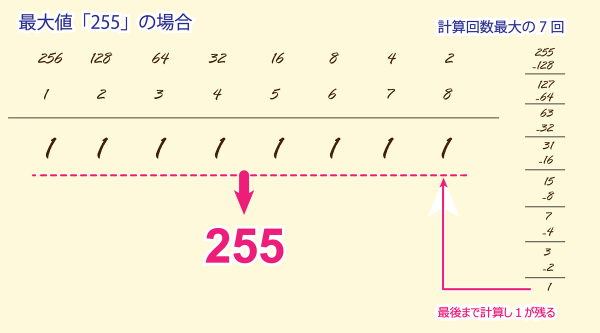
「２５５」の場合
最大値で答えが「11111111」になるので、
これは手間がかかりそうと直感で感じますね。
まさに、計算回数最大の７回で「11111111」が求まります。
12_「２５５」の場合
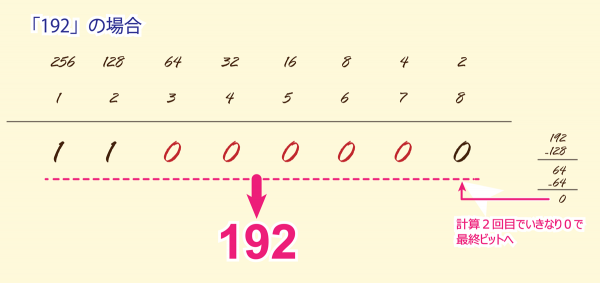
「１９２」の場合
よく見るプライベートネットワークで見る
「192.168.0.0」の「１９２」です。
ビットパターンを知っていると「11000000」という
すっきりしたパターンだと思うわけですが、
計算でそんなのが出るのか？
そう疑いたくなるわけですが、
計算２回目でいきなり「０」となって、
最終ビットにセットして終了。
「11000000」が求まります。
13_「１９２」の場合
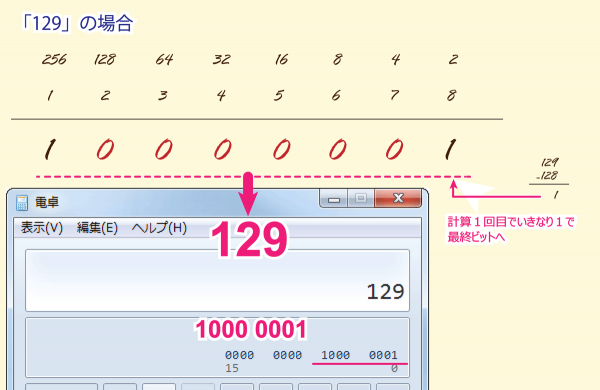
「１２９」の場合
では、また面白いビットパターンとして、
「１２９」というのもあります。
これは「10000001」というビットになります。
計算してみると、そうですね。
１回目で余りが「１」で最終ビットに「１」を立てて終了。
14_「１２９」の場合
ちょっと気持ちいいと思いませんか？
さいごに
どうです？
面倒なのは「２５５」位で、
少なくとも７回の計算で正確にビットパターンが求められます。
手で指折り求められる人はいいとして、
紙上で計算して求められるので、後から見直すこともできます。
ちょっとビットパターンを求めてみたくなりませんか？
プログラムを書いたりしていて、
検算をしたりなどを繰り返しているうちに、
偶然この方法を見つけたのですが、
これって既に有名な方法なんですかね？
本サイトで公開しているツールについては、
十分にテストは行っておりますが個人で作成している為、
潜在的なバグがないとは言い切れません。
その為、ツールを用いた結果については十分検証の上ご利用ください。
当サイトおよび、管理人は如何なる損害もその責を負いません。
当サイト内のコンテンツおよび画像において、
出典・引用の外部著作権者の明記がないものは、
すべて管理人による著作物です。
当サイトでご紹介しておりますコンテンツの著作権の放棄は致しません。
サイト内コンテンツを引用される際にはご連絡は不要です。
ただし、出典元として当サイト(個別記事)へのリンクをお願いいたします。
申し訳ございませんが、無断転載、複製をお断りさせて頂いております。
コンテンツを有益であると感じていただけましたら非常に光栄です。
ありがとうございます。
公開日：
最終更新日：2019/06/20
