8桁のビットパターンを紙とペンで10進数に変換する方法
IPアドレスやサブネットマスクなどの値を2進数に戻して、
計算した後に再び10進数に戻すような場合には、
紙とペンがあれば簡単に2進数を10進数に戻すことができます。
ここではその手順についてご紹介します。
IPアドレスの問題やネットワーク関連の問題では、
10進数・2進数変換を良く利用します。
とても頻繁に利用するのですが、試験などでは電卓やツールが使えず、
暗算で求める必要があったりと慣れるまでは難しいものです。
目次
8桁のビットパターンを紙とペンで10進数に変換する方法
変換の手順をご紹介する前に、
簡単な例で10進数をまず2進数に変換してみます。
10進数を2進数にする際も紙とペンで簡単に求められます。
2の乗数とビットパターンの関係
まず、2の2乗である4はビットパターンにするとどうなるでしょうか。
0(10進数) ⇒ 0(2進数)
1(10進数) ⇒ 1(2進数)
2(10進数) ⇒ 10(2進数)
3(10進数) ⇒ 11(2進数)
4(10進数) ⇒ 100(2進数)
では、2の3乗の8は?
4(10進数) ⇒ 100(2進数)
5(10進数) ⇒ 101(2進数)
6(10進数) ⇒ 110(2進数)
7(10進数) ⇒ 111(2進数)
8(10進数) ⇒ 1000(2進数)
気付きましたか?
2の乗数だと、乗数(2乗・3乗)の数に一致する数の「0」と、
繰り上がった桁に「1」があります。
では、2の8乗(256)は?
計算する必要もありませんね。
「100000000」です(1が1つと0が8つ)
この法則については以下でご紹介しました。
サブネットマスクなどでよく見る「255」という数字。
これはまさに、この「256-1=255」です。
256で1繰り上がって9桁になっているこのビットから、
繰り上がる前のー1をした値を考えると、
「11111111」が255なのはすぐに想像がつきますね。
サブネットマスク「255.255.255.0」なんかは、
「11111111.11111111.11111111.00000000」だと分かります。
2の乗数のビットパターンから10進数に戻す
さて、では今までは2の乗数とビットパターンの関係を見てきました。
ですので、
もう「100000」と見れば、
0が5つあるな・・・2の5乗と言うことだな。
なら「32」だとすぐに求めることができます。
2の5乗が32だって電卓もなく計算できない?
そこは呪文を唱えて指折り求めるんです。
任意のビットパターンから10進数に戻す
では、ここからが本題です。
「10101010」というビットパターンを
10進数に戻したい場合には、どうしますか?
※ここではIPアドレスに関しての処理なので8bit(8桁)を前提とします。
求める手順を順を追ってご紹介します。
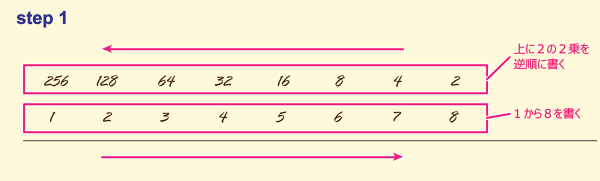
STEP1
まず、左から1~8の数字を書きます。
次にその上にでも、右から2の乗数を順に書きます。
この値を利用して計算していきます。
STEP2
①次に求めたいビットパターンを番号の下に書きます。
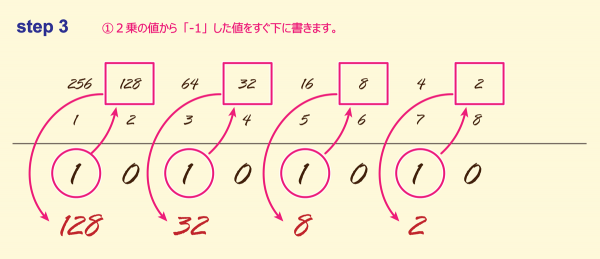
STEP3
①1を書いた部分の下に一つ右の乗数値を書きます。
STEP4
①書いた乗数の値をすべて足します。
②合計して求めた値が、10進数に戻した値です。
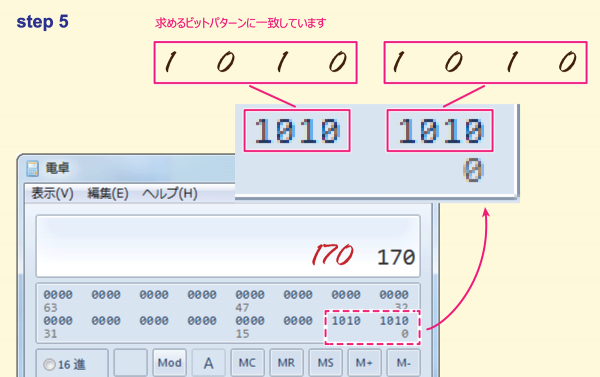
STEP5
練習では検算をWindows電卓などを利用して行うといいでしょう。
Windows電卓でビットパターンを確認する方法は以下でご紹介しています。
本当かいな?という方へ
まぁ、私も何となくこの方法を見つけた時は、
本当かいなと思ったのですが、ちゃんと求められるんですね。
以下は疑い深い方向けに・・・
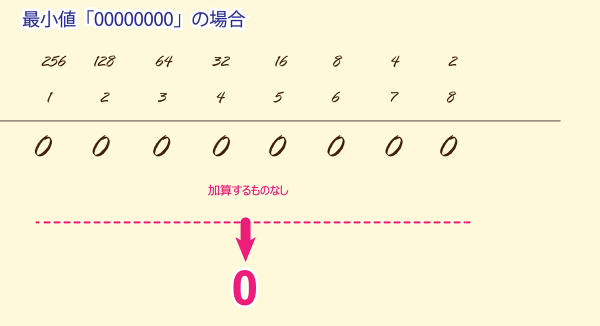
「00000000」の場合
当然、1が一つもないので何も加算するものがありません。
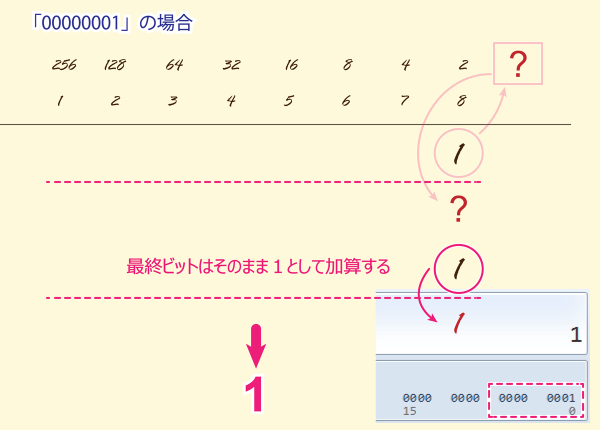
「00000001」の場合
1の場合は?
一つ右に乗数した値がありません。何を加算しましょうか?
最終ビットに1が立っている場合には、そのまま下に「1」を書きます。
結果「1」となります。
これは1に関わらず、その他の値でも同じです。
最終ビットはそのまま下に1を書く。
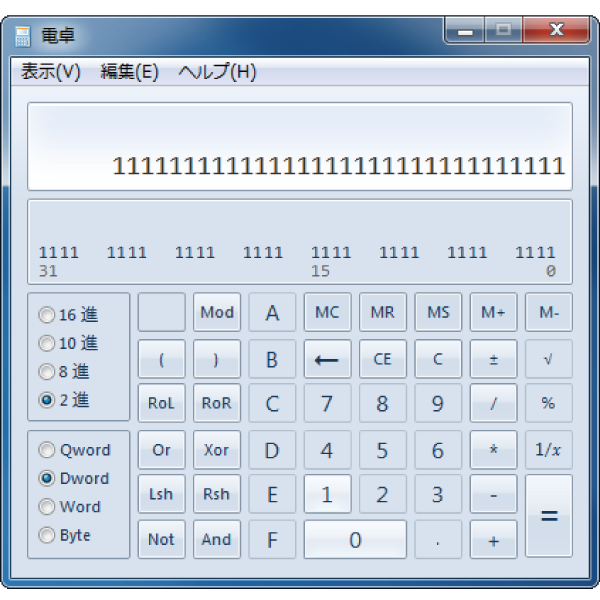
「11111111」の場合
これが一番計算数の多いパターンです。
まぁ、先ほどの「10000000(256)- 1 = 255」とインド式のような、
計算方法を利用したほうが楽ですし、
「11111111」は計算するまでもなく「255」と覚えてしまうでしょうけど。
このルールで計算しても正しく求まります。
「10000001」の場合
最終ビットに「1」が立ったこのパターンはどうでしょう。
正しく求められます。
「11000000」の場合
よく目にする(10進数として)このビットパターンはどうでしょう。
正しく求められます。
プライベートアドレスでよく見かける「192.168.0.0」の192です。
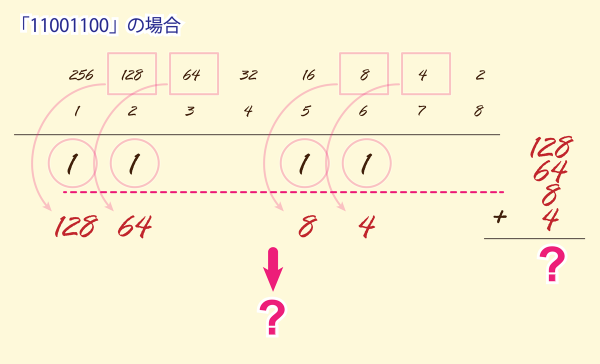
「11001100」の場合
では「11001100」の場合はどうでしょうか。
ちょっと足し算してみて下さい。
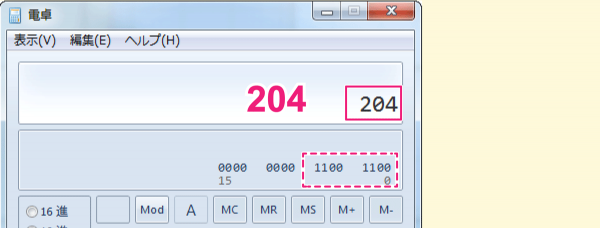
答えは以下です。
ちょっとすぐに求められたら便利だと思いませんか?
さいごに
どうです?
面倒なのは「255」位で、すべて足し算で求められます。
手で指折り求められる人はいいとして、
紙上で計算して求められるので、後から見直すこともできます。
ちょっとビットパターンが簡単に感じることができませんか?
プログラムを書いたりしていて、
検算をしたりなどを繰り返しているうちに、
偶然この方法を見つけたのですが、
これも既に有名な方法なんですかね?
本サイトで公開しているツールについては、
十分にテストは行っておりますが個人で作成している為、
潜在的なバグがないとは言い切れません。
その為、ツールを用いた結果については十分検証の上ご利用ください。
当サイトおよび、管理人は如何なる損害もその責を負いません。
当サイト内のコンテンツおよび画像において、
出典・引用の外部著作権者の明記がないものは、
すべて管理人による著作物です。
当サイトでご紹介しておりますコンテンツの著作権の放棄は致しません。
サイト内コンテンツを引用される際にはご連絡は不要です。
ただし、出典元として当サイト(個別記事)へのリンクをお願いいたします。
申し訳ございませんが、無断転載、複製をお断りさせて頂いております。
コンテンツを有益であると感じていただけましたら非常に光栄です。
ありがとうございます。
公開日:
最終更新日:2019/06/20